Let ABCD be a rectangle. Let P, Q, R, S be the mid-points of sides
Let ABCD be a rectangle. Let P, Q, R, S be the mid-points of sides AB, BC, CD, DA respectively. Then the quadrilateral PQRS is a
- Square
- Rectangle, but need not be a square
- Rhombus, but need not be a square
- Parallelogram, but need not be a rhombus
Answer
A rhombus is a parallelogram with all sides equal.
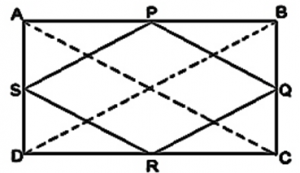
In ΔABC, P and Q are the mid-points of AB and BC respectively.
∴ PQ || AC and PQ = ½AC (Mid-point theorem)
Similarly in ΔADC, SR || AC and SR = ½AC (Mid-point theorem)
So, PQ || SR and PQ = SR
Since in quadrilateral PQRS, one pair of opposite sides is equal and parallel to each other, it is a parallelogram.
∴ PS || QR and PS = QR (Opposite sides of parallelogram)
In ΔBCD, Q and R are the mid-points of side BC and CD respectively.
∴ QR || BD and QR = ½BD (Mid-point theorem)
However, the diagonals of a rectangle are equal.
∴ AC = BD
PQ = QR = SR = PS
Therefore, PQRS is a rhombus.
The correct option is C.